Si han escuchado o leído sobre Fibonacci y se preguntan ¿para qué sirve la sucesión de fibonacci?, sea por curiosidad, estudios o lo que fuera siempre es bueno conocer respecto a la secuencia de Fibonacci y para qué sirve.

¿Qué es la sucesión de fibonacci?
La Secuencia De Fibonacci, es una sucesión de números que, sin explicación, y para muchos de forma misteriosa, suele aparecer en diferentes aspectos de la naturaleza. Dicha secuencia fue definida hacia fines del siglo XII precisamente por el italiano Leonardo Fibonacci.
En lo que hace a lo matemático la secuencia es infinita, y se inicia en 0 y 1. Los números subsiguientes corresponde siempre a la suma de los dos números anteriores. Por lo que, después de 0 y 1, aparecen 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144. etc.
¿Para qué sirve la sucesión de fibonacci?
La secuencia de Fibonacci y la geometría
Si convertimos los números en cuadrados, los ubicamos y nos permite trazar un espiral perfecto, el que aparece en organismos vivos así como los términos de la frecuencia permiten definir a la “proporción áurea”, utilizada en el arte y arquitectura, en especial a nivel visual por su atractivo. Aquí encontrarás más info sobre ¿Cómo utilizar la secuencia Fibonacci?
Por lo que, en matemáticas, la sucesión o serie de Fibonacci se refiere a la secuencia ordenada de números que describió Leonardo de Pisa, Leonardo Pisano o Leonardo Bigollo (c. 1170 - 1250), también conocido como Fibonacci, un matemático italiano del siglo XII. Así a cada uno de los elementos/números de la serie Fibonacci se le da el nombre de número de Fibonacci.
Formulación de Fibonacci
Fibonacci describió dicha sucesión ejemplificándola como la solución a un problema de cría de conejos señalando que: “Cierto hombre tiene una pareja de conejos juntos en un lugar cerrado y desea saber cuántos son creados a partir de este par en un año cuando, de acuerdo a su naturaleza, cada pareja necesita un mes para envejecer y cada mes posterior procrea otra pareja”.
- Partimos de una pareja de conejos el primer mes
- El segundo mes la pareja envejece pero no procrea
- El tercer mes la pareja procrea otra pareja (es decir, ya tenemos 2 parejas)
- El cuarto mes, la primera pareja vuelve a procrear y la pareja nueva envejece sin procrear (luego tenemos 3 parejas)
- El quinto mes, las dos parejas más viejas vuelven a procrear mientras que la nueva pareja no procrea (siendo 5 parejas en total).
Números de Fibonacci reflejados en matemáticas
¿Qué es el Número áureo?
Llamado número áureo, también denominado número de oro o divina proporción, corresponde al valor numérico de la proporción que tienen entre sí dos segmentos de recta a y b (siendo "a" más largo que "b"); la longitud total es al segmento a, como a es al segmento b.
Existen varias propiedades, entre ellas la del propio número, su cuadrado y su inverso tienen entre sí las mismas cifras decimales, como se refleja en esta fórmula:
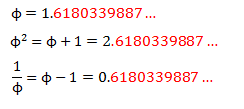
Otro aspecto en cuánto a los números de Fibonacci es la llamada razón o cociente entre un término de Fibonacci y el inmediatamente anterior, que se modifica de forma constante, para estabilizarse recién en el número áureo:

¿Qué es el Triángulo de Pascal?
El llamado triángulo de Pascal representa los coeficientes binomiales ordenados en forma triangular. Así cada fila del triángulo equivale a los coeficientes de los monomios que figuran en el desarrollo del binomio (a + b) n (tomando el 1 de arriba como la potencia n = 0), es decir los coeficientes que figuran en el binomio de Newton son coincidentes respecto a los elementos de cada fila del triángulo de Pascal.
Construcción del triángulo de Pascal:
Ubicar un 1 en el vértice superior del triángulo.
En la fila inferior, colocar un 1 a la derecha y un 1s a la izquierda del 1 de arriba.
En las filas inferiores, colocar 1 en los extremos
En las posiciones intermedias colocar la suma de los números inmediatamente superiores.

Propiedades del triángulo de Pascal:
Al incluirle los elementos de cada fila se obtienen las potencias de 2: 1, 2, 4, 8, 16,…
Al sumarle dos elementos consecutivos de la diagonal 1-3-6-10-15-… se obtiene un cuadrado perfecto: 1, 4, 9, 16, 25,…
En La fila el primer número después del 1 que es un número primo siendo que todos los demás números son divisibles por dicho número primo (excluyendo los 1s claro). Si en la fila 1-7-21-35-35-21-7-1 el primer número después del 1 es el 7, que es primo. Y en los demás números, 35, 21 y 7, siendo todos divisibles por 7.
Calcular los números de la secuencia de Fibonacci
No hay una única manera de calcular los números de la secuencia de Fibonacci, existiendo diferentes ejemplos como los que veremos:
Al iniciar desde los números 0 y 1, los números de Fibonacci quedan definidos de la siguiente manera:
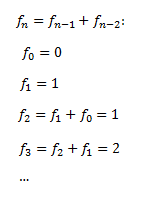
La Función Generadora; es la función que permite la sucesión pudiendo ser cualquiera a0, a1, a2,… es la función f(X) = a0 + a1x + a2x2+…, equivale a una serie formal de potencias en la que cada coeficiente corresponde a un elemento de la sucesión. Los números de Fibonacci disponen de la función generadora reflejada en la siguiente fórmula:
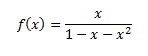
La Fórmula explícita; es la forma para calcular los números de Fibonacci utilizando la expresión del número áureo reflejada en la siguiente fórmula:
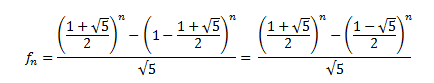
Les guste las matemáticas y geometría o no la secuencia de Fibonacci tiene su atractivo y misterio por así decirlo, si bien los amantes de los números son los que mejor saben apreciarlo.



